Định Nghĩa, Tính Chất & Cách Chứng Minh Tam Giác Vuông Lớp 7, 8, 9
Tam giác vuông là gì? Tam giác vuông là tam giác bao gồm một góc vuông (90°). Luân chuyển quanh chuyên đề kỹ năng về tam giác vuông có rất nhiều điều thú vị để chúng ta khám phá. Bao gồm: những khái niệm, tính chất, định lý, cách chứng tỏ tam giác vuông,… Chúng có mối tương tác qua lại cùng với nhau, chế tạo ra nền tảng quan trọng để các bạn học xuất sắc toán hình. Bạn đang xem: Cách chứng minh tam giác vuông lớp 7
Ở bài viết này, gia sư Thành Tâm sẽ lần lượt đáp án một giải pháp chi tiết, dễ nắm bắt nhất những vấn đề định hướng và bài xích tập của tam giác vuông. Hãy cùng đọc và tham khảo nhé!

Nội dung bài xích viết ẨN
1. Tổng quan lại về tam giác vuông
2. Những định lý vào tam giác vuông
2.1. Định lý Pytago (Tính độ nhiều năm cạnh)
2.2. Phương pháp tính diện tích tam giác vuông
2.3. Hệ thức lượng vào tam giác vuông
2.4. Đường cao vào tam giác vuông
2.5. Đường trung con đường trong tam giác vuông
3. Vệt hiệu nhận biết tam giác vuông
4. Cách chứng minh tam giác vuông
5. Bài tập chứng tỏ tam giác vuông
Tổng quan lại về tam giác vuông
Tam giác vuông là tam giác bao gồm một góc vuông.
Một tam giác vuông có:
Cạnh huyền: Cạnh đối lập với góc vuông.Cạnh góc vuông: Là hai cạnh kề của góc vuông.Đường cao: là mặt đường thẳng nối từ bỏ đỉnh và vuông góc cùng với cạnh đối diện.Đường trung tuyến: là mặt đường thẳng nối từ đỉnh và đi qua trung điểm của cạnh đối diện.Các định lý vào tam giác vuông
Tam giác vuông là một trong những trong những tam giác quánh biệt, vì vậy nó bao gồm biểu thức tính cấp tốc về độ dài các cạnh, diện tích s tam giác, độ dài con đường cao, đường trung tuyến, nửa đường kính đường tròn nội tiếp với ngoại tiếp,…
Định lý Pytago (Tính độ lâu năm cạnh)
Trong một tam giác vuông, bình phương cạnh huyền bằng tổng nhị cạnh góc vuông. Chũm thể:
c² = a² + b²
Trong đó:
a, b: là độ lâu năm hai cạnh góc vuôngc: là độ lâu năm cạnh huyềnVí dụ: Tam giác ABC vuông tại A, lúc đó: BC² = AB² + AC²
Công thức tính diện tích tam giác vuông
Diện tích tam giác vuông được tính bằng những công thức bên dưới đây:
S = 1/2 (a.b) = 1/2.c.h
Trong đó:
a, b: Độ nhiều năm hai cạnh góc vuông.c: Độ dài cạnh huyềnh: Độ dài chiều cao ứng với cạnh huyền.Ví dụ: đến tam giác vuông ABC vuông trên A, lúc đó diện tích tam giác vuông ABC bằng:
S = 1/2.AB.AC = 1/2.AH.BC
Hệ thức lượng vào tam giác vuông
Gia sư dạy dỗ toán lý hóa 8 của thành tâm xin giữ hộ đến các bạn một số bí quyết hệ thức lượng trong tam giác vuông. Việc ghi nhớ, vận dụng thông thạo những công thức này sẽ giúp chúng ta học tốt cả về hình học phẳng cùng hình học không gian (lớp 11, 12).
Cụ thể:
AC² = HC.BCAB² = HB.HCAH.BC = AB.BC1/AH² = 1/AB² + 1/AC²BC² = AB² + AC²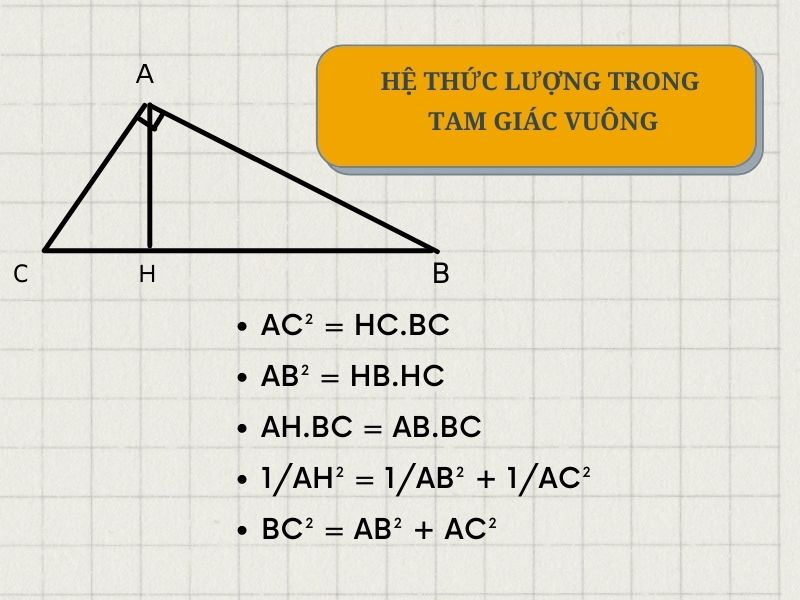
Đường cao trong tam giác vuông
Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích nhị hình chiếu của nhị cạnh góc vuông bên trên cạnh huyền.
Đường trung con đường trong tam giác vuông
Trong tam giác vuông, đường trung con đường ứng cùng với cạnh huyền bởi một nửa cạnh huyền.
Dấu hiệu nhận thấy tam giác vuông
Tam giác gồm một góc vuông là tam giác vuông.Tam giác vuông gồm hai góc nhọn phụ nhau là tam giác vuông.Tam giác bao gồm bình phương độ nhiều năm một cạnh bởi tổng bình phương độ dài hai cạnh là tam giác vuông. (Định lý Pytago đảo)Tam giác gồm đường trung con đường ứng với một cạnh bởi nửa cạnh ấy là tam giác vuông.Tam giác nội tiếp đường tròn bao gồm một cạnh là 2 lần bán kính là tam giác vuông.Cách chứng minh tam giác vuông
Chứng minh tam giác vuông hay triệu chứng minh bất kỳ loại hình học nào thì cũng vậy, thông thường các bạn dựa vào vết hiệu nhận biết của chúng để chứng minh.
Thông thường sẽ có được 4 cách minh chứng tam giác vuông như sau:
Cách 1: phụ thuộc vào định lý Pytago đảo: Tam giác có bình phương độ nhiều năm một cạnh bởi tổng bình phương độ dài hai cạnh là tam giác vuông.Ví dụ: Tam giác ABC có: BC² = AB² + AC² thì tam giác ABC vuông trên A
Cách 2: Tam giác bao gồm hai góc phụ nhau (Tổng nhì góc nhọn vào một tam giác là 90º)Ví dụ: Tam giác ABC có góc A + B = 90º thì tam giác ABC vuông trên C.
Cách 3: minh chứng đường trung tuyến đường ứng với cạnh huyền bằng một nửa cạnh huyền.Ví dụ: Tam giác ABC gồm M là trung điểm của cạnh BC với AM = 1/2BC ⇒ Tam giác ABC vuông tại A.
Cách 4: chứng minh tam giác kia nội tiếp mặt đường tròn và gồm một cạnh là 2 lần bán kính của mặt đường tròn.Ví dụ: Tam giá chỉ ABC nội tiếp con đường tròn (O) và có cạnh BC là đường kính (BC=2R) ⇒ Tam giác ABC là tam giác vuông tại A.

Bài tập chứng tỏ tam giác vuông
Bài 1: mang lại tam giác ABC có BC = 8cm, AC = 17cm với BC = 8cm.
a/ chứng tỏ tam giác ABC là tam giác vuông.
b/ trên tia đối của tia BC mang điểm D, sao để cho BD = 8cm. Tính độ dài AD và chứng minh AD = BC.
Bài 2: mang đến tam giác vuông ABC gồm AB = 5cm, AC = 12cm, BC = 13cm.
Xem thêm: Cách Chụp Hình Máy Tính Có Thể Bạn Đã Bỏ Lỡ, 3 Cách Chụp Màn Hình Máy Tính Windows Nhanh Chóng
a/ minh chứng tam giác ABC vuông trên A với tính độ dài con đường cao AH.
b/ Kẻ HE vuông góc với AB trên E, HF vuông góc cùng với AC tại F. Bệnh minh: AE.AB = AF.AC
Bài 3: mang đến tam giác ABC vuông tại A, mặt đường cao AH, biết HB = 3,6cm, HC = 6.4cm.
a/ Tính độ dài cạnh AB, AC và AH.
b/ Kẻ HE vuông góc với AB tại E, HF vuông góc với AC trên F. Hội chứng minh: AE.AB = AF.AC
Bài 4: mang lại tam giác ABC vuông tại A, đường cao AH. Trường đoản cú H kẻ HD cùng HE lần lượt vuông góc với AC. Vẽ trung tuyến đường AM.
Chứng minh:
a/ DE = AH
b/ Góc BAM = góc DAM, góc ADM = góc ACB
c/ AM vuông góc cùng với DE
KẾT LUẬN:
Gia sư toán lớp 7 của Thành Tâm mong muốn qua bài viết này, các các bạn sẽ lần lượt đáp án được đa số thắc mắc của chính bản thân mình về lý thuyết, bài tập cùng cách chứng tỏ tam giác vuông cụ thể nhất. Mỗi chăm đề kiến thức và kỹ năng điều bao gồm điều thú vị với “điểm” khó riêng. Toán học là môn tất cả tính kế thừa, vì vậy, các bạn nên học dĩ nhiên và nắm vững kiến thức.
Đến đây, sẽ có tương đối nhiều bạn thắc mắc: “Có giải pháp nào nhằm nhớ nhanh những công thức hệ thức lượng cùng định lý vào tam giác vuông không?” Câu trả lời là không. Mỗi các bạn sẽ có một phương thức học riêng và phải làm bài tập thiệt nhiều thì mới ghi nhớ được công thức.
Chúc các bạn học tốt!
Mọi chi tiết và vướng mắc vui lòng liên hệ về số hotline 0374771705 hoặc fanpage để được tư vấn và hướng dẫn.
Tam giác vuông là gì? Tam giác vuông là tam giác gồm một góc vuông (90°). Chuyển phiên quanh chuyên đề kiến thức và kỹ năng về tam giác vuông có nhiều điều thú vui để chúng ta khám phá. Bao gồm: các khái niệm, tính chất, định lý, cách chứng tỏ tam giác vuông,… Chúng có mối tương tác qua lại cùng với nhau, chế tạo nền tảng đặc trưng để các bạn học giỏi toán hình.
Ở bài viết này, gia sư Thành Tâm vẫn lần lượt giải đáp một giải pháp chi tiết, dễ hiểu nhất các vấn đề lý thuyết và bài tập của tam giác vuông. Hãy thuộc đọc và xem thêm nhé!


Bài tập chứng tỏ tam giác vuông
Bài 1: đến tam giác ABC bao gồm BC = 8cm, AC = 17cm và BC = 8cm.
a/ chứng tỏ tam giác ABC là tam giác vuông.
b/ trên tia đối của tia BC lấy điểm D, làm sao cho BD = 8cm. Tính độ nhiều năm AD và chứng minh AD = BC.
Bài 2: mang lại tam giác vuông ABC bao gồm AB = 5cm, AC = 12cm, BC = 13cm.
a/ chứng tỏ tam giác ABC vuông tại A và tính độ dài đường cao AH.
b/ Kẻ HE vuông góc với AB tại E, HF vuông góc cùng với AC tại F. Hội chứng minh: AE.AB = AF.AC
Bài 3: đến tam giác ABC vuông trên A, mặt đường cao AH, biết HB = 3,6cm, HC = 6.4cm.
a/ Tính độ lâu năm cạnh AB, AC và AH.
b/ Kẻ HE vuông góc cùng với AB trên E, HF vuông góc cùng với AC tại F. Triệu chứng minh: AE.AB = AF.AC
Bài 4: mang lại tam giác ABC vuông trên A, mặt đường cao AH. Tự H kẻ HD với HE theo thứ tự vuông góc cùng với AC. Vẽ trung tuyến AM.
Chứng minh:
a/ DE = AH
b/ Góc BAM = góc DAM, góc ADM = góc ACB
c/ AM vuông góc cùng với DE
KẾT LUẬN:
Gia sư toán lớp 7 của Thành Tâm hy vọng qua nội dung bài viết này, các các bạn sẽ lần lượt giải đáp được mọi thắc mắc của chính mình về lý thuyết, bài tập và cách chứng minh tam giác vuông cụ thể nhất. Mỗi chăm đề kiến thức điều bao hàm điều thú vị với “điểm” nặng nề riêng. Toán học là môn gồm tính kế thừa, vày vậy, các bạn nên học vững chắc và nắm vững kiến thức.
Đến đây, sẽ có khá nhiều bạn thắc mắc: “Có bí quyết nào nhằm nhớ nhanh những công thức hệ thức lượng và định lý trong tam giác vuông không?” Câu vấn đáp là không. Mỗi các bạn sẽ có một phương thức học riêng biệt và cần làm bài bác tập thiệt nhiều thì mới ghi nhớ được công thức.
Chúc chúng ta học tốt!
Mọi cụ thể và thắc mắc vui lòng contact về số hotline 0374771705 hoặc fanpage để được tư vấn và phía dẫn.









