CÁCH CHỨNG MINH 4 ĐIỂM CÙNG THUỘC 1 ĐƯỜNG TRÒN CỰC HAY, CÁCH CHỨNG MINH 4 ĐIỂM CÙNG THUỘC MỘT ĐƯỜNG TRÒN
Chứng minh những điểm (thường là 4 điểm) thuộc thuộc một con đường tròn là dạng bài tập thịnh hành thường chạm chán trong những bài toán liên quan đến tứ giác và con đường tròn.
Bạn đang xem: Cách chứng minh 4 điểm cùng thuộc 1 đường tròn
Vậy cách chứng tỏ các điểm (4 điểm) trực thuộc được tròn như vậy nào? có mấy cách chứng tỏ 4 điểm cùng thuộc một con đường tròn? họ cùng khám phá qua bài viết dưới đây nhé.
° Phương pháp chứng tỏ các điểm nằm trong một con đường tròn
* biện pháp 1: Chứng minh các điểm kia cùng cách đều một điểm O vậy định. Lúc đó những điểm đã cho cùng thuộc đường tròn trọng tâm O.
* phương pháp 2: Sử dụng tứ giác nội tiếp. Ví dụ điển hình để chứng tỏ 5 điểm A, B, C, D, E cùng thuộc một đường tròn ta minh chứng ABCD, ABCE là tứ giác nội tiếp thuộc 1 mặt đường tròn trọng tâm O.
Dưới đây, chúng ta cùng tham khảo một số ví dụ minh họa cách bệnh mình 4 điểm cùng thuộc đường tròn.
* lấy ví dụ như 1: Cho tam giác ABC vuông trên A, mặt đường cao AH. Tự M là vấn đề bất kì bên trên cạnh BC kẻ MD ⊥ AB, ME ⊥ AC. Minh chứng 5 điểm A, D, M, H, E cùng nằm trên một đường tròn.
* Lời giải:
- Theo bài xích ra, tất cả có hình sau: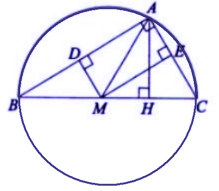
Xét tam giác vuông ADM có cạnh huyền AM
Xét tam giác vuông AEM có cạnh huyền AM
Và tam giác vuông AHM có cạnh huyền AM
Các tam giác này phần đa có chung cạnh huyền AM đề xuất 3 đỉnh góc vuông nằm trên tuyến đường tròn đường kính AM tất cả tâm là trung điểm của AM.
Vậy 5 điểm A, D, M, H, E thuộc nằm bên trên một con đường tròn.
* ví dụ như 2: Cho tam giác ABC vuông trên A gọi D là điểm đối xứng cùng với A qua cạnh BC. Chứng tỏ 4 điểm A, B, C, D thuộc thuộc một con đường tròn.
* Lời giải:
- Ta tất cả hình vẽ như sau:

Vì D đối xứng cùng với A qua BC, B đối xứng cùng với B qua BC, C đối xứng với C qua BC nên
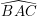
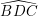
Suy ra ∠BDC = ∠BAC = 900
Xét tam giác vuông BAC và BDC có chung cạnh huyền BC nên hai đỉnh góc vuông A, D nằm trên tuyến đường tròn 2 lần bán kính BC, bao gồm tâm là trung điểm của cạnh huyền BC.
Vậy 4 điểm A, B, C, D cùng nằm bên trên một mặt đường tròn.
* lấy một ví dụ 3: Cho tam giác ABC vuông tại A. Bên trên AC mang điểm D. Hình chiếu của D lên BC là E, điểm đối xứng của E qua BD là F. Minh chứng 5 điểm A, B, E, D, F cùng nằm trên một mặt đường tròn. Xác minh tâm O của con đường tròn đó.
* Lời giải:
- Ta tất cả hình vẽ như sau:
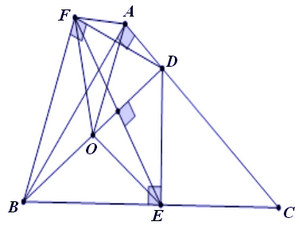
- bởi E cùng F đối xứng với nhau qua BD phải BD là mặt đường trung trực của đoạn thẳng EF cần suy ra:
BF = BE và DF = DE
Suy ra: ΔBFD = ΔBED (c-c-c)
Suy ra: ∠BFD = ∠BEB = 900
- điện thoại tư vấn O là trung điểm của BD.
- Xét tam giác vuông ABD vuông trên A tất cả AO là trung tuyến đường nên:
AO = ½BD = OB = OD (1)
- Xét tam giác vuông BDE vuông trên E bao gồm OE là trung đường nên:
EO = ½BD = OB = OD (2)
- Xét tam giác vuông BFD vuông tại F gồm OF là trung con đường nên:
FO = ½BD = OB = OD (3)
Từ (1), (2) cùng (3) suy ra: OA = OB = OD = OE = OF.
Vậy 5 điểm A, B, E, D, F thuộc nằm bên trên một con đường tròn tâm O cùng với O là trung điểm của BC.
Hy vọng với bài bác viết Cách minh chứng các điểm (4 điểm) cùng thuộc một đường tròn ở nội dung toán lớp 9 trên của hayhochoi.vn giúp những em giải các bài tập dạng này một bí quyết dễ dàng. Hầu như góp ý với thắc mắc những em hãy để lại nhận xét dưới nội dung bài viết để Hay học tập Hỏi ghi nhận với hỗ trợ, chúc những em học tập tốt.
Bạn sẽ xem: Cách minh chứng các điểm (4 điểm) thuộc thuộc một mặt đường tròn – Toán 9 chăm đề trên kynanggame.edu.vnChứng minh những điểm (thường là 4 điểm) cùng thuộc một đường tròn là dạng bài xích tập thông dụng thường gặp gỡ trong những bài toán liên quan đến tứ giác và con đường tròn.
Vậy cách minh chứng các điểm (4 điểm) thuộc vòng thi như thế nào? tất cả bao nhiêu cách chứng tỏ 4 điểm thuộc thuộc một mặt đường tròn? Hãy cùng tò mò qua bài viết dưới đây.
° phương pháp chứng minh những điểm thuộc con đường tròn
* bí quyết 1: Chứng minh rằng những điểm này biện pháp đều một điểm cố định O. Lúc đó các điểm đã mang lại nằm trê tuyến phố tròn vai trung phong O.
* giải pháp 2: Sử dụng tứ giác nội tiếp. Chẳng hạn, để chứng tỏ 5 điểm A, B, C, D, E thuộc thuộc một đường tròn, ta chứng minh ABCD, ABCE là những tứ giác nội tiếp trong đường tròn trung khu O.
Dưới đây bọn họ cùng tham khảo một vài ví dụ minh họa để chứng minh 4 điểm cùng thuộc một mặt đường tròn.
* ví dụ như 1: Cho tam giác ABC vuông trên A, đường cao AH. Vì M là 1 điểm bất kỳ trên cạnh BC, vẽ MD ⊥ AB, ME ⊥ AC. Chứng tỏ rằng 5 điểm A, D, M, H, E cùng nằm bên trên một con đường tròn.
* Trả lời:
Theo bài bác báo thì có hình sau:
Xét tam giác vuông ADM bao gồm cạnh huyền AM
Xét tam giác vuông AEM tất cả cạnh huyền AM
Và tam giác vuông AHM bao gồm cạnh huyền AM
Các tam giác này đều sở hữu chung cạnh huyền AM phải 3 đỉnh của góc vuông nằm trên phố tròn đường kính AM tất cả tâm là trung điểm AM.
Vậy 5 điểm A, D, M, H, E cùng nằm trên một đường tròn.
* lấy một ví dụ 2: Cho tam giác ABC vuông tại A, gọi D là vấn đề đối xứng cùng với A qua cạnh BC. Chứng minh 4 điểm A, B, C, D cùng thuộc một đường tròn.
* Trả lời:
Ta tất cả hình sau:

Vì D đối xứng cùng với A qua BC, B đối xứng với B qua BC, với C đối xứng với C qua BC, đề xuất

Suy ra BDC = BAC = 900
Xét tam giác vuông BAC cùng BDC tất cả chung cạnh huyền BC buộc phải hai đỉnh của góc vuông A và D nằm trên tuyến đường tròn 2 lần bán kính BC, tâm là trung điểm của cạnh huyền BC.
Vậy 4 điểm A, B, C, D cùng thuộc một mặt đường tròn.
* lấy một ví dụ 3: đến tam giác ABC vuông tại A. Bên trên AC đem điểm D. Hình chiếu của D trên BC là E, điểm đối xứng của E qua BD là F. Minh chứng rằng 5 điểm A, B, E, D, F thẳng hàng . Một điểm. Vòng tròn. Tìm vai trung phong O của mặt đường tròn.
* Trả lời:
Ta tất cả hình sau:

– vì chưng E cùng F đối xứng nhau qua BD, BD là trung trực của đoạn trực tiếp EF cần suy ra:
BF = BE và DF = DE
Suy ra: BFD = GIƯỜNG (ccc)
Suy ra: BFD = BEB = 900
– điện thoại tư vấn O là trung điểm của BD.
– Xét tam giác vuông ABD vuông trên A tất cả AO là trung tuyến đường nên:
AO = BD = OB = OD (1)
– Xét tam giác vuông BDE vuông trên E gồm OE là trung con đường nên:
EO = BD = OB = OD (2)
– Xét tam giác vuông BFD vuông tại F có trung tuyến đường OF nên:
FO = BD = OB = OD (3)
Từ (1), (2) cùng (3) suy ra: OA = OB = OD = OE = OF.
Vậy 5 điểm A, B, E, D, F nằm trên phố tròn trung khu O với O là trung điểm của BC.
Hi vọng với nội dung bài viết Cách chứng tỏ các điểm (4 điểm) cùng thuộc một mặt đường tròn thuộc nội dung toán lớp 9 trên của ngôi trường PHÒNG GIÁO DỤC ĐÀO TẠO HUYỆN TRẠM TẤU đang giúp chúng ta giải các bài tập này một bí quyết dễ dàng. đa số góp ý và thắc mắc chúng ta vui lòng nhằm lại comment bên dưới nội dung bài viết để tuyệt Học ghi nhận với hỗ trợ, chúc chúng ta đạt hiệu quả học tập tốt nhất.
Đăng bởi: PHÒNG GIÁO DỤC ĐÀO TẠO HUYỆN TRẠM TẤU
Bản quyền bài viết thuộc về ngôi trường kynanggame.edu.vn. Mọi xào nấu đều là gian lận! Nguồn chia sẻ: PHÒNG GIÁO DỤC ĐÀO TẠO HUYỆN TRẠM TẤU (kynanggame.edu.vn) Tags toán lớp 9
Nhớ nhằm nguồn nội dung bài viết này: Cách minh chứng các điểm (4 điểm) thuộc thuộc một con đường tròn – Toán 9 chăm đề của trang web kynanggame.edu.vn









