Lý Thuyết Hình Hộp Đứng Là Gì ? Tính Chất Và Các Công Thức Tính
Hình chóp, hình lăng trụ, hình hộp là đều hình cơ bạn dạng trong hình học tập không gian. Đa số những bài toán nghỉ ngơi cấp thpt đều thao tác làm việc trên những hình này. Để hoàn toàn có thể giải quyết được các bài toán ko gian, cách đầu chúng ta ta buộc phải hiểu được đà nào là hình chóp, hình lăng trụ tuyệt hình hộp.
Bạn đang xem: Hình hộp đứng là gì
1. Hình chóp
Hình chóp là gì?
Cho nhiều giác $A_1A_2A_3… A_n$ phía bên trong mặt phẳng $(P)$ với một điểm $S$ nằm ngoại hình phẳng $(P)$. Nối $S$ với các đỉnh của đa giác ta được $n$ miền tam giác $SA_1A_2, SA_2A_3,…, SA_n
A_1$. Hình tạo bởi $n$ tam giác đó với đa giác $A_1A_2A_3… A_n$ hotline là hình chóp và kí hiệu là $S.A_1A_2A_3… A_n$.
Trong đó:
$S$ được goi là đỉnh của hình chóp;$A_1A_2A_3… A_n$ là mặt đáy của hình chóp;$SA_1, SA_2,…, SA_n$ là các bên cạnh của hình chóp;A1A2, A2A3,…, An
A1 là những cạnh đáy của hình chiếu;Các miền tam giác $SA_1A_2, SA_2A_3,…, SA_n
A_1$ là mặt mặt của hình chóp.
Cách hotline tên hình chóp bằng tên của đỉnh với mặt đáy, ví dụ như hình vẽ sau là hình chóp $S.ABCDE$ hoặc cụ thể hơn là hình chóp ngũ giác $S.ABCDE$
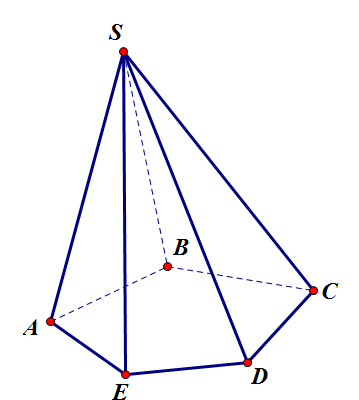
Đường cao của hình chóp là mặt đường vuông góc kẻ trường đoản cú đỉnh của hình chóp mang lại mặt đáy.
Hình tứ diện
Cho tứ điểm A, B, C, D không đồng phẳng. Hình có bốn tam giác ABC, BCD, CDA, ABD hotline là tứ diện ABCD.
A, B, C, D là các đỉnh của tứ diện;AB, BC, CD, CA là các kề bên của tứ diện;Các tam giác ABC, BCD, CDA, ABD là các mặt mặt của tứ diện;Hai cạnh ko đi qua 1 đỉnh được call là nhì cạnh đối nhau;Đỉnh ko nằm bên trên một khía cạnh được hotline là đỉnh đối lập với khía cạnh đó.
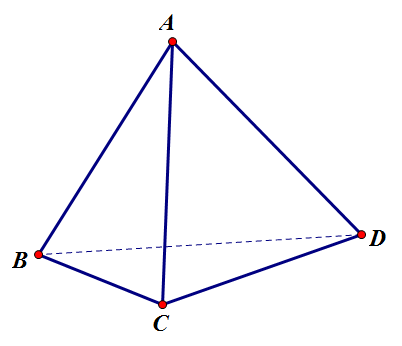
Hình chóp cùng hình tứ diện đều phải có 4 đỉnh, 4 mặt cùng 6 cạnh như nhau, tuy nhiên hình chóp gồm phân biệt mặt mặt và mặt đáy, trong lúc hình tứ diện thì ko quy ước điện thoại tư vấn đâu là phương diện đáy, đâu là phương diện bên.
Hình chóp đều
Định nghĩa: Hình chóp phần đa là hình chóp có các lân cận bằng nhau và mặt đáy là một nhiều giác đều.Tính chất: trong hình chóp đều, chân đường cao của hình chóp trùng với trung ương đường tròn nước ngoài tiếp nhiều giác đáy.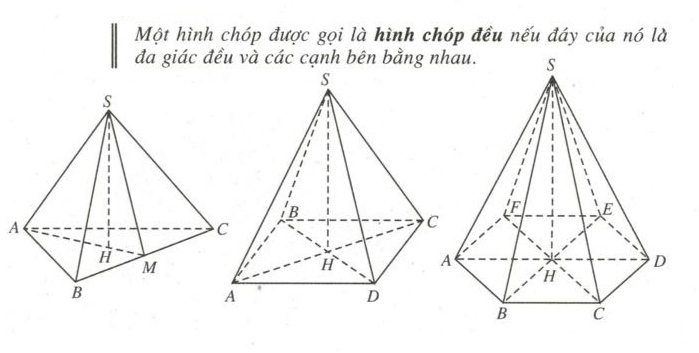
Như vậy, từ quan niệm suy ra:
Hình chóp là hình chóp hồ hết khi còn chỉ khi đáy của nó là nhiều giác đều và chân con đường cao của nó trùng với trung ương của đa giác đáy.Hình chóp là hình chóp hồ hết khi còn chỉ khi đáy của chính nó là đa giác rất nhiều và các lân cận tạo với mặt dưới các góc bằng nhau.
2. Hình chóp cụt
Hình chóp cụt
Hình chóp cụt đều
Cho hình chóp cụt đa số $S.A_1A_2…A_n$. Một khía cạnh phẳng $(P)$ tuy vậy song với dưới đáy cắt các bên cạnh $SA_1, SA_2,…,SA_n$ theo lần lượt tại $A’_1, A’_2,…, A’_n$. Phần hình nằm giữa đáy cùng mặt phẳng $(P)$ hotline là hình chóp đều.
Đa giác $A_1A_2A_3… A_n$ với thiết diện $A’_1A’_2A’_3… A’_n$ điện thoại tư vấn là hai mặt đáy;Các hình thang cân nặng $A_1A’_1A’_2A_2,…, A_n
A’_n
A’_1A_1$ là các mặt bên;Đoạn thẳng nối hai trọng điểm O với O’ của hai đáy điện thoại tư vấn là đường cao của hình chóp cụt đều.
3. Hình lăng trụ
Hình lăng trụ là gì?
Hình hợp bởi các hình bình hành $A_1A’_1A’_2A_2,A_2A_3A’_3A’_2…, A_n
A’_n
A’_1A_1$ và hai miền nhiều giác $A_1A_2A_3… A_n; A’_1A’_2A’_3… A’_n$ phía trong hai khía cạnh phẳng song song đươc goi là hình lăng trụ.
Các hình bình hành $A_1A’_1A’_2A_2,A_2A_3A’_3A’_2…, A_n
A’_n
A’_1A_1$ là những mặt bên;Hai miền đa giác $A_1A_2A_3… A_n; A’_1A’_2A’_3… A’_n$ là hai mặt dưới (hai hình đa giác này bởi nhau);Các đoạn trực tiếp $A_1A’_1,…, A_n
A’_n$ là những cạnh bên;Các đoạn thẳng $A_1A_2,A’_1A’_2,…, A_n
A_1, A’_n
A’_1$ là các cạnh lòng của hình lăng trụ.
Ký hiệu hình lăng trụ: $A_1A_2…A_n.A’_1A’_2…A’_n$.
Gọi tên lăng trụ theo tên những đa giác đáy: Lăng trụ tam giác (có đáy là tam giác), lăng trụ tứ giác (có lòng là tứ giác),…
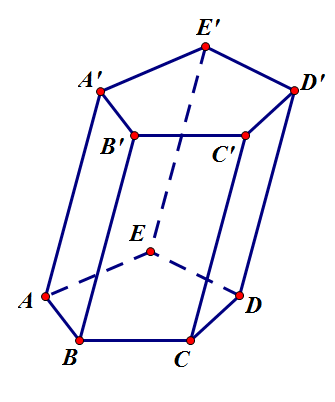
Hình lăng trụ đứng
Hình lăng trụ đứng là hình lăng trụ có các sát bên vuông góc với phương diện đáy.Nhận xét: những mặt bên của hình lăng trụ đứng là những hình chữ nhật với vuông góc với khía cạnh đáy.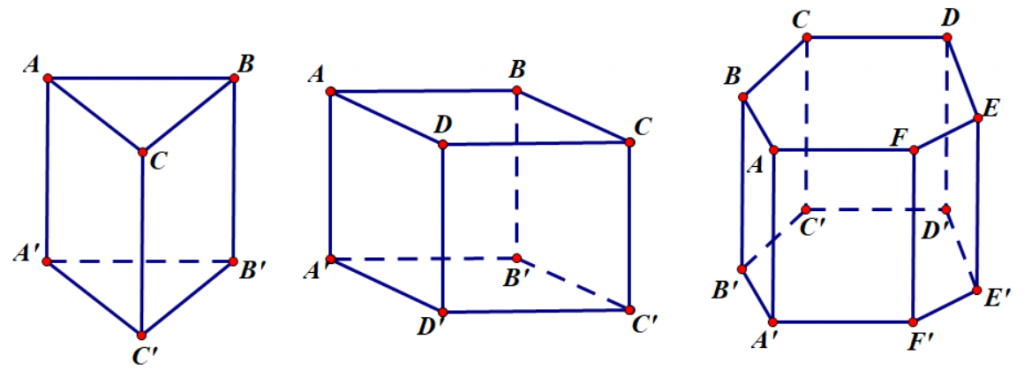
Hình lăng trụ đều
Hình lăng trụ đều là hình lăng trụ đứng tất cả đáy là nhiều giác đều.Nhận xét: Các phương diện bên của hình lăng trụ những là các hình chữ nhật bằng nhau. Ngoài ra, hình lăng trụ đều phải sở hữu các đặc điểm của hình lăng trụ đứng.4. Hình hộp
Hình hộp là gì?
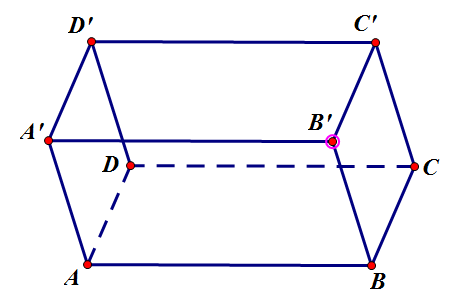
Hình lăng trụ tứ giác tất cả đáy là hình bình hành được hotline là hình hộp.
Sáu mặt (bốn mặt mặt và nhì mặt đáy) các là những hình bình hành.Mỗi mặt có một mặt tuy vậy song cùng với nó, nhì mặt như vậy gọi là nhì mặt đối diện.
Hình vỏ hộp đứng
Hình hộp đứng là hình lăng trụ đứng có đáy là hình bình hành.Nhận xét: Trong hình vỏ hộp đứng có bốn mặt bên là hình chữ nhật.Hình hộp chữ nhật
Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật.
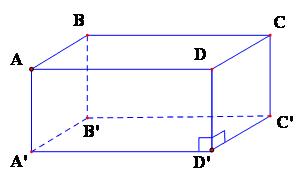
Nhận xét: Tất cả sáu khía cạnh của hình vỏ hộp chữ nhật gần như là hình chữ nhật.
Hình lập phương
Hình lập phương là hình hộp có tất cả sáu khía cạnh là hình vuông. (Các hình vuông vắn này bằng nhau).
Xem thêm: Định Nghĩa Hiện Tượng Tự Nhiên Là Gì ? Hiện Tượng Tự Nhiên
Hình lăng trụ đứng được phát âm là gì? Đặc điểm nhận ngoài mặt lăng trụ đứng như vậy nào? Và cách tính diện tích tương tự như thể tích của hình lăng trụ đứng bằng phương pháp như nào? nội dung bài viết dưới đây, chúng tôi sẽ giúp các em học viên nắm kiên cố một những thiết kế khá phổ biến trong số những dạng hình về khối lăng trụ, kia là kỹ năng và kiến thức về hình lăng trụ đứng và những dạng bài xích tập có ích từ cơ bạn dạng đến nâng cao. Để các em học sinh rất có thể vận dụng sau bài xích học.
Hình lăng trụ đứng được đọc là gì?
Theo như định nghĩa, thì hình lăng trụ chính là hình nhiều diện và bao hàm 2 đáy nằm trên 2 mặt phẳng tuy vậy song với nhau và cũng chính là 2 nhiều giác bằng nhau. Theo đó thì 2 đáy này có thể là hình vuông, hình bình hành, tương tự như hình tam giác hoặc hình chữ nhật,…
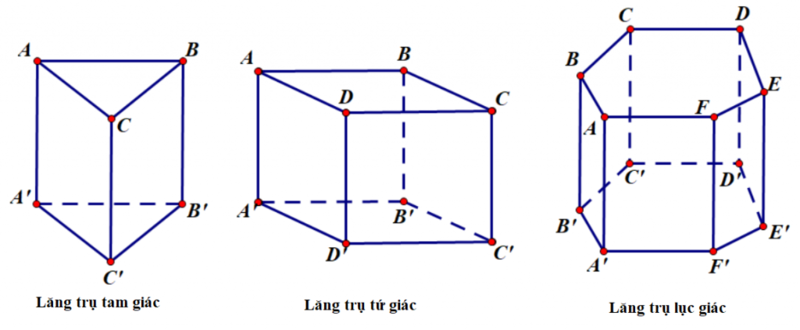
Đồng thời thì những mặt bên chính là hình bình hành và gồm các ở kề bên bằng và tuy vậy song với nhau. Theo như tư tưởng về hình lăng trụ, thì hình lăng trụ đứng thiết yếu sẽ là hình có:
Hai lòng của hình lăng trụ này là hai đa giác phẳng hoặc là bởi nhau, nằm ở 2 phương diện phẳng tuy vậy song cùng với nhau.Những mặt bên của hình lăng trụ đứng này đang vuông góc với rất nhiều mặt phẳng bao gồm chứa những đa giác bên dưới đáy. Đối cùng với hình lăng trụ đứng này, thì các mặt mặt sẽ đó là những hình chữ nhật.Các đặc điểm của hình lăng trụ đứng
Đối với hình học lăng trụ đứng này, trong chương trình trung học phổ thông các bạn học sinh đã có được tiếp cận những định hướng cơ bản. Từ có mang cơ bản có thể tiện lợi đưa ra được những tính chất của hình lăng trụ đứng:
Đây chính là loại hình lăng trụ đứng sẽ sở hữu những kề bên nằm vuông góc với đáy.
Tất cả đầy đủ mặt mặt của hình lăng trụ đứng này sẽ chính là hình chữ nhật.Hình lăng trụ đứng bao gồm mặt phẳng cất đáy là phần đông mặt phẳng tuy nhiên song cùng với nhau.Cạnh bên đó là chiều cao của hình lăng trụ đứng.Đây chính là tính chất đặc trưng để phân biệt cũng giống như nhận biết hình lăng trụ đứng với những hình lăng trụ khác. Gần như hình lăng trụ đứng này sẽ có đáy là phần đông hình bình hành còn được biết đến với tên gọi chính là hình vỏ hộp đứng.

Những hình lăng trụ đứng bao gồm đáy là hình bình hành thường sẽ được biết đến với một tên thường gọi khác đó chính là hình hộp đứng. Đối với hình lăng trụ dạng đứng có đáy là hình tam giác hay là hình tứ giác thì đều sẽ tiến hành gọi là hình lăng trụ tam giác gần như hoặc hình lăng trụ tứ giác đều. Như vậy tên gọi của mỗi những thiết kế sẽ dựa theo tên của đa giác đáy mà các bạn gọi tên.
Công thức tính diện tích xung xung quanh và bí quyết thể tích
Diện tích xung quanh của hình lăng trụ dạng đứng
Diện tích bao bọc của một hình lăng trụ dạng đứng sẽ được tính bằng cách lấy chu vi lòng của hình lăng trụ nhân với chiều cao h. Vào đó, độ cao của hình lăng trụ dạng đứng đó là độ dài cạnh bên.
Công thức bao quát đúng nhất:
Sxq = 2p.h
Trong đó:
p: nửa chu vi của đáy
h: chiều cao.
Để hoàn toàn có thể tính diện tích toàn phần của loại hình lăng trụ đứng này, thì chúng ta học sinh bắt buộc tính tổng diện tích xung quanh và ăn mặc tích của hai đáy hình lăng trụ.
Công thức nhằm tính diện tích s hình lăng trụ đứng toàn phần sẽ bằng tổng của diện tích s hai đáy và diện tích xung quanh.
Stp = Sxq + 2 S đáy
Thể tích của hình lăng trụ dạng đứng
Thể tích của hình lăng trụ dạng đứng sẽ được tính bằng tích diện tích s đáy nhân với chiều cao của hình lăng trụ dạng đứng.
Công thức tổng quát:
V = S.h
Trong đó:
S: diện tích s đáy
h: chiều cao hình lăng trụ đứng.
Một số hình lăng trụ đứng đặc biệt

Hình lăng trụ đứng
– Định nghĩa: Hình hộp dạng đứng là hình hộp có cạnh bên vuông góc với khía cạnh đáy.
– đặc điểm của hình lăng trụ: Hình vỏ hộp đứng thì sẽ sở hữu được 2 đáy là hình bình hành, với 4 mặt bao quanh là 4 hình chữ nhật.
Hình hộp chữ nhật
– Định nghĩa: Hình hộp chữ nhật đó là hình vỏ hộp đứng tất cả đáy là hình chữ nhật.
– Tính chất: Hình vỏ hộp chữ nhật sẽ có được 6 mặt là 6 hình chữ nhật.
+) Hình chữ nhật sẽ sở hữu 12 cạnh, 8 đỉnh và có 6 mặt.
+) các đường chéo cánh sẽ bao gồm hai đầu mút là 2 đỉnh đối nhau của hình vỏ hộp chữ nhật đồng quy trên một điểm duy nhất
+) diện tích của nhị mặt đối lập trong hình vỏ hộp chữ nhật đang là bởi nhau
+) Chu vi của hình chữ nhật gồm hai mặt đối lập trong hình vỏ hộp chữ nhật bởi nhau
Hình lập phương
– Định nghĩa: Hình lập phương chính là hình vỏ hộp chữ nhật 2 đáy và sẽ là 4 mặt mặt đều là hình vuông.
– Tính chất: Hình lập phương đều có 6 mặt mọi là hình vuông.
+) Khối lập phương chính là hình đa diện đều một số loại 4; 3. Những mặt chính là hình vuông, từng đỉnh đang là đỉnh chung của 3 mặt.
+) Khối lập phương đều sở hữu 6 mặt, 8 đỉnh cùng 12 cạnh.
Kết luận
Qua những thông tin trên shop chúng tôi đã tổng hợp số đông kiến thức kim chỉ nan về hình lăng trụ đứng cũng như bí quyết tính diện tích s và thể tích hình. Hy vọng nội dung bài viết này sẽ là phần đông tài liệu cũng là kiến thức hữu dụng dành cho các bạn học sinh. Việc những em học thật chắc kỹ năng cơ bạn dạng và tiếp đến sẽ vận dụng vào bài xích tập là điều cần thiết nhất. Các em học viên hãy thường xuyên ôn luyện để có thể giải các dạng bài tập hình lăng trụ đứng này cấp tốc hơn cùng đúng hơn, chắc chắn sẽ giúp ích cho các kỳ thi nhé.









