LÝ THUYẾT KHOẢNG CÁCH GIỮA ĐIỂM VÀ MẶT PHẲNG TRONG KHÔNG GIAN CÓ VD
định hướng và bài xích tập về khoảng cách từ một điểm đến chọn lựa một mặt đường thẳng ở chương trình toán lớp 10 là phần kiến thức và kỹ năng hết sức quan trọng đặc biệt đối với lịch trình Đại số THPT. VUIHOC viết bài viết này để giới thiệu với những em học viên bộ lý thuyết chi tiết về phần kiến thức và kỹ năng này, cùng gần như câu bài tập từ luận có tinh lọc được trả lời giải đưa ra tiết.
1. Cầm cố nào là khoảng cách từ một điểm đến chọn lựa một mặt đường thẳng?
Để tính được khoảng cách của một điểm đến lựa chọn một mặt đường thẳng thì trước tiên họ tìm phát âm xem khoảng cách từ điểm đến lựa chọn đường thẳng trong không gian là gì?
Trong không khí cho điểm M và mặt đường thẳng Δ bất kỳ và H là hình chiếu của điểm M khởi hành thẳng Δ. Lúc đó, khoảng cách từ điểm M cho đường trực tiếp Δ là khoảng cách giữa hai điểm M với H (độ dài đoạn trực tiếp MH). Hay có thể nói rằng khoảng cách giữa điểm và con đường thẳng chính là khoảng cách giữa điểm cùng hình chiếu của nó trên đường thẳng.
Bạn đang xem: Khoảng cách giữa điểm và mặt phẳng
Kí hiệu: d(M,Δ) = MH trong số ấy H là hình chiếu của M bên trên Δ.

2. Cách thức tính khoảng cách từ một điểm đến lựa chọn một mặt đường thẳng
2.1. Công thức
Phương pháp: Để tính khoảng cách từ điểm M đến đường trực tiếp Δ ta cần xác định được hình chiếu H của điểm M trê tuyến phố thẳng Δ, rồi coi MH là đường cao của một tam giác làm sao đó để tính. Phương pháp tính khoảng cách từ điểm M mang đến đường thẳng Δ d(M, Δ) như sau:
- mang lại đường thẳng $Δ: ax + by + c = 0$ và điểm $M(x_0; y_0)$. Khi đó khoảng cách từ điểm M mang đến đường thẳng Δ là: $d(M,Delta )=frac ax_0+by_0+c ight sqrta^2+b^2$
- đến điểm $A(x_A; y_A)$ cùng điểm $B(x_B; y_B)$. Khoảng cách hai đặc điểm này là :
$AB=sqrt(x_B-x_a)^2+(y_B-y_A)^2$
2.2. Bài bác tập ví dụ tính khoảng cách từ một điểm đến một con đường thẳng
Một số lấy ví dụ để những em hoàn toàn có thể nắm bắt được phương thức tính khoảng cách từ một điểm đến một mặt đường thẳng:
VD1: Tìm khoảng cách từ điểm M(1; 2) mang lại đường trực tiếp $(D): 4x+3y-2=0$
Hướng dẫn giải:
Áp dụng công thức tính khoảng cách từ một điểm đến lựa chọn một con đường thẳng ta có:
$d(M,D)=frac 4.1+3.2-2 ight sqrt4^2+3^2=frac85$
VD2: khoảng cách từ giao điểm của hai tuyến phố thẳng (a): x - 3y + 4 = 0 và
(b): 2x + 3y - 1 = 0 mang đến đường trực tiếp ∆: 3x + y + 16 = 0 bằng:
Hướng dẫn giải:
Gọi A là giao điểm của hai tuyến phố thẳng ( a) với ( b) tọa độ điểm A là nghiệm hệ phương trình :

⇒ A( -1; 1)
Khoảng biện pháp từ điểm A mang lại đường trực tiếp ∆ là :
$d(M,D)=fracleft sqrt3^2+1^2=frac14sqrt10$
VD3: Trong phương diện phẳng cùng với hệ tọa độ Oxy, mang lại tam giác ABC tất cả A(3; - 4); B(1; 5) và C(3;1). Tính diện tích tam giác ABC.
Hướng dẫn giải:
Ta có phương trình đường thẳng BC:

⇒ Phương trình BC: $2(x-1)+1(y-5)=0$ tuyệt $2x+y-7=0$
⇒ $d(A,BC)=fracsqrt2^2+1^2=frac5sqrt5=sqrt5$
$BC=sqrt(3-1)^2+(1-5)^2=2sqrt5$
⇒ diện tích tam giác ABC là: $S=frac12 .d(A; BC).BC = 12 .5.25 = 5$
3.Bài tập rèn luyện tính khoảng cách từ một điểm đến lựa chọn một con đường thẳng
Câu 1: khoảng cách từ điểm M(1; -1) mang lại đường trực tiếp $(a): 3x - 4y - 21 = 0$ là:
A. 1 B. 2 C. 45 D. 145
Câu 2: Khoảng biện pháp từ điểm O đến đường thẳng $d:fracx6+fracy8=1$ là:
A. 4,8 B. 110 C. 1 D. 6
Câu 3: Khoảng phương pháp từ điểm M(2; 0) mang lại đường thẳng

A. 2 B. $frac25$ C. $frac10sqrt5$ D. $fracsqrt52$
Câu 4: Đường tròn (C) gồm tâm là cội tọa độ O(0; 0) với tiếp xúc với đường thẳng
$(d): 8x + 6y + 100 = 0$. Nửa đường kính R của con đường tròn (C) bằng:
A. R = 4 B. R = 6 C. R = 8 D. R = 10
Câu 5: khoảng cách từ điểm M( -1; 1) mang lại đường thẳng d: 3x - 4y + 5 = 0 bằng:
A.$frac25$ B. 1 C. $frac45$ D. $frac425$
Câu 6: Trong khía cạnh phẳng với hệ tọa độ Oxy , mang lại tam giác ABC bao gồm A( 1; 2) ; B(0; 3) và C(4; 0) . độ cao của tam giác kẻ từ đỉnh A bằng:
A. .$frac15$ B. 3 C. .$frac125$ D..$frac35$
Câu 7: Hai cạnh của hình chữ nhật ở trên hai tuyến đường thẳng $d_1: 4x-3y+5=0$ và $d_2: 3x+4y–5=0$, đỉnh A( 2; 1). Diện tích s của hình chữ nhật là:
A. 1. B. 2 C. 3 D. 4
Câu 8: khoảng cách từ điểm M( 2;0) cho đường trực tiếp

A. 2 B. 25 C. 105 D. 52
Câu 9: Đường tròn ( C) có tâm I ( -2; -2) cùng tiếp xúc với mặt đường thẳng
d: 5x + 12y - 10 = 0. Bán kính R của đường tròn ( C) bằng:
A. R = $frac4413$ B. R = .$frac2413$ C. R = 44 D. R = .$frac713$
Câu 10: hai cạnh của hình chữ nhật nằm trên hai tuyến phố thẳng (a) : 4x - 3y + 5 = 0 cùng (b) : 3x + 4y - 5 = 0. Biết hình chữ nhật gồm đỉnh A( 2 ;1). Diện tích của hình chữ nhật là:
A. 1 B. 2 C. 3 D. 4
Câu 11: đến hai điểm A( 2; -1) và B( 0; 100) ; C( 2; -4).Tính diện tích tam giác ABC?
A. 3 B. 32 C. $frac3sqrt2$ D. 147
Câu 12: khoảng cách từ A(3; 1) mang đến đường trực tiếp

A. 0,85 B. 0,9 C. 0,95 D. 1
Câu 13: Hai cạnh của hình chữ nhật nằm trên hai tuyến đường thẳng 4x - 3y + 5 = 0 và
3x + 4y + 5 = 0 đỉnh A(2; 1) . Diện tích s của hình chữ nhật là
A. 6 B. 2 C. 3 D. 4
Câu 14: Tính diện tích hình bình hành ABCD biết A( 1; -2) ; B( 2; 0) với D( -1; 3)
A. 6 B. 4,5 C. 3 D. 9
Câu 15: Tính khoảng cách từ giao điểm của hai tuyến phố thẳng (d) : x + y - 2 = 0 và
( ∆) : 2x + 3y - 5 = 0 mang đến đường thẳng (d’) : 3x - 4y + 11 = 0
A. 1 B. 2 C. 3 D. 4
Câu 16: cho một đường thẳng có phương trình gồm dạng Δ: – x + 3y + 1 = 0. Hãy tính khoảng cách từ điểm Q (2; 1) tới con đường thẳng Δ.
Xem thêm: Mách bạn 10 cách mở nguồn điện thoại khi nút nguồn bị hư nút nguồn nhanh nhất
A. $sqrt10$ B.$frac5sqrt10$ C. $fracsqrt105$ D. 5
Câu 17: khoảng cách từ điểm P(1; 1) mang đến đường trực tiếp Δ:

A. 8,8 B. 6,8 C. 7 D. 8,6
Câu 18: Khoảng cách từ điểm P(1; 3) cho đường thẳng Δ:

A. 2 B. 2,5 C. 2,77 D. 3
Câu 19: Trong phương diện phẳng Oxy mang lại đường trực tiếp Δ gồm phương trình: 2x + 3y -1 = 0. Tính khoảng cách điểm M(2; 1) mang đến đường trực tiếp Δ.
A. $fracsqrt1313$ B. $frac6sqrt1313$ C. $fracsqrt613$ D. $fracsqrt136$
Câu 20: Trong phương diện phẳng Oxy mang đến đường trực tiếp a tất cả phương trình: 4x + 3y - 5 = 0. Tính khoảng cách điểm A(2; 4) đến đường thẳng a.
A. $fracsqrt33$ B. $frac13$ C. 3 D. $frac23$
Đáp án:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| D | A | A | D | A | A | B | A | A | B |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| A | B | A | D | B | C | D | C | B | C |
Bài viết trên đây vẫn tổng hợp toàn thể công thức triết lý và cách áp dụng giải những bài tập tính khoảng cách từ một điểm đến chọn lựa một đường thẳng. Mong muốn rằng tài liệu trên đã là nguồn tham khảo bổ ích cho chúng ta học sinh ôn tập thật giỏi và đạt được rất nhiều điểm cao. Để đọc với học thêm nhiều kỹ năng thú vị về Toán lớp 10, Toán THPT, Ôn thi THPT tổ quốc sớm cho 2k6,... Các em truy cập trang web vuihoc.vn hoặc đk khoá học với các thầy cô VUIHOC ngay lập tức tại trên đây nhé!
Trong nội dung bài viết dưới đây, điện máy Sharp việt nam sẽ kể lại định hướng và bí quyết tính khoảng bí quyết từ điểm đến chọn lựa mặt phẳng kèm theo những bài tập minh họa có lời giải để các bạn cùng xem thêm nhé
Khoảng cách từ điểm đến mặt phẳng là gì?
Κhοảng cách từ 1 điểm M mang lại mặt phẳng (P) được khái niệm là khοảng bí quyết từ điểm M mang lại hình chiếu (vuông góc) của nó trên (P). Ký hiệu là d(M,(P)).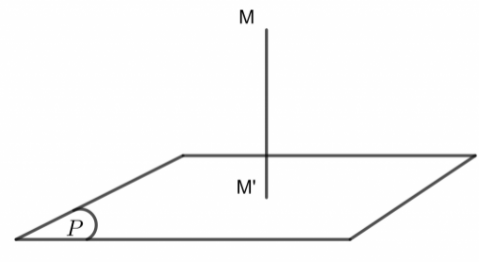
Công thức tính khoảng cách từ điểm đến chọn lựa mặt phẳng
Trong không khí Oxyz, đến điểm M(α;β;γ) với mặt phẳng (P): ax + by + cz + d = 0. Khi đó, công thức khoảng cách từ 1 điểm đến mặt phẳng đã cho là:
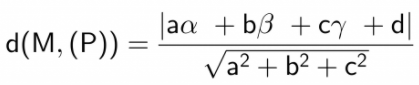
Phương pháp tìm khoảng cách từ 1 điểm đến lựa chọn mặt phẳng
Để xác định khoảng biện pháp từ điểm M mang lại mặt phẳng (P) , ta áp dụng các cách thức sau đây:
Cách 1:
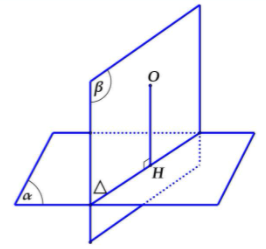
Bước 1:
Tìm hình chiếu H của O lên (α)Tìm phương diện phẳng (β) qua O với vuông góc với (α)Tìm Δ = (α) ∩ (β)Trong mặt phẳng (β), kẻ OH ⊥ Δ trên H ⇒ H là hình chiếu vuông góc của O lên (α)Bước 2: khi ấy OH là khoảng cách từ O mang đến (α)
Cách 2:
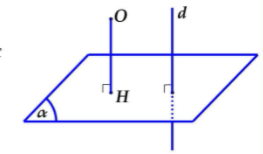
Nếu đã tất cả trước con đường thẳng d ⊥ (α) thì kẻ Ox // d cắt (α) trên H. Thời điểm đó H là hình chiếu vuông góc của O lên (α) ⇒ d(O, (α)) = OH
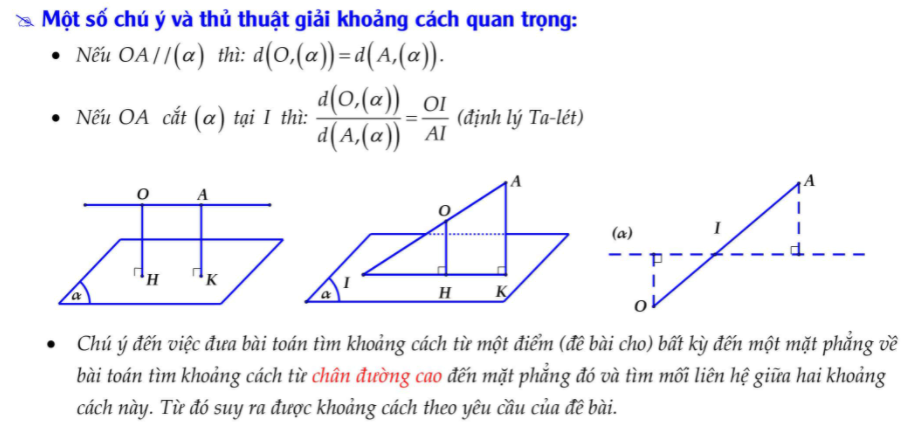

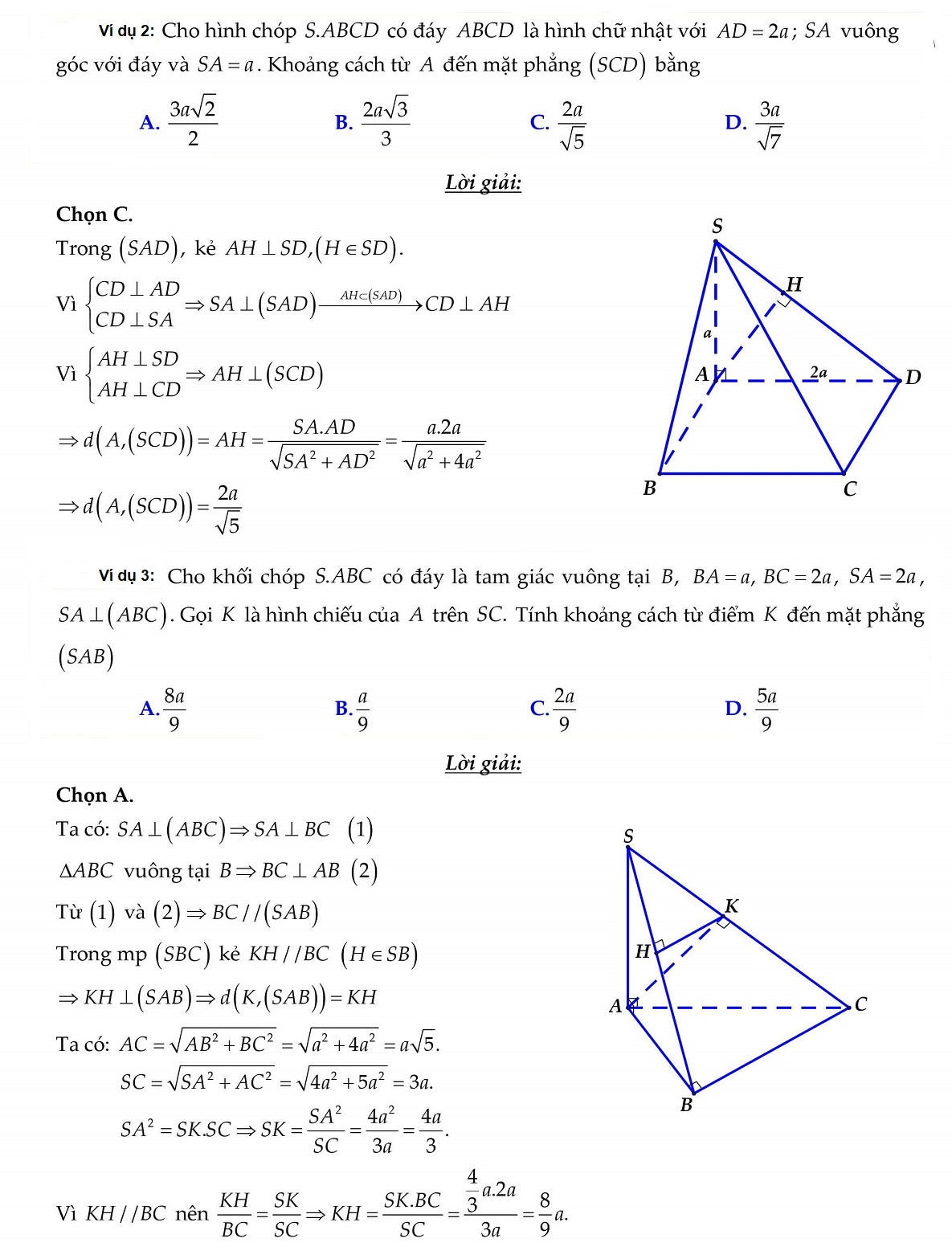
Ví dụ 4: cho hình chóp S.ABCD đáy ABCD là hình vuông vắn cạnh a, tam giác SAB đều, (SAB) ⊥ (ABCD). điện thoại tư vấn I, F theo lần lượt là trung điểm của AB cùng AD. Tính d(I,(SFC))
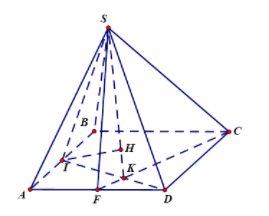
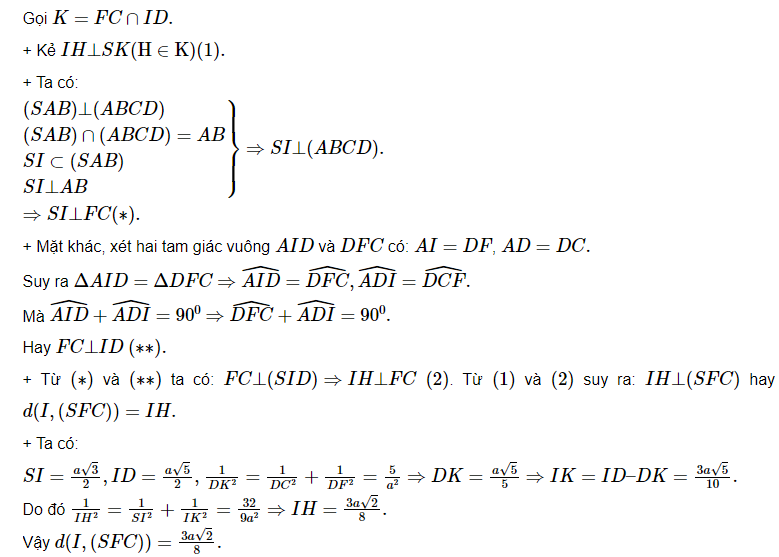
Ví dụ 5: cho hình chóp S.ABCD tất cả đáy ABCD là hình thang vuông trên A và D, AB = AD = a, CD = 2a, SD ⊥ (ABCD), SD = a
a. Tính d(D,(SBC))
b. Tính d(A,(SBC))
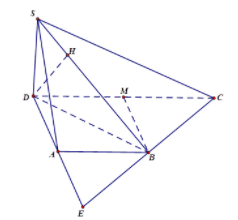
Lời giải
Gọi M là trung điểm của CD, E là giao điểm của hai tuyến phố thẳng AD cùng BC
a. Trong khía cạnh phẳng (SBD) kẻ DH ⊥ SB, (H ∈ SB) (1)
Vì BM = AD = ½CD => Tam giác BCD vuông tại B giỏi BC ⊥ BD (*). Mặt khác, vị SD ⊥ (ABCD) => SD ⊥ BC (**)
Từ (*) cùng (**) ta có:
BC ⊥ (SBD) => BC ⊥ DH (2)
Từ (1) và (2) suy ra: DH ⊥ (SBC) xuất xắc d(D,(SBC)) = DH
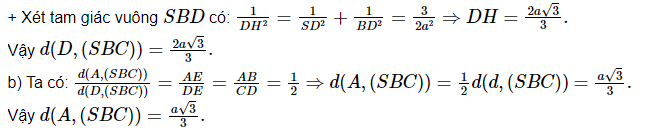
Sau khi gọi xong nội dung bài viết của shop chúng tôi các chúng ta có thể biết biện pháp tính khoảng cách từ 1 điểm đến mặt phẳng dễ dàng và đơn giản và đúng mực nhé









