Diện Tích Xung Quanh Là Gì, Công Thức Tính Diện Tích Xung Quanh Hình Nón
b) Quy tắc: Giử sử hình vỏ hộp chữ nhật tất cả chiều dài là (a), chiều rộng là (b) và chiều cao là (h).
Bạn đang xem: Diện tích xung quanh là gì
- mong mỏi tính diện tích s xung quanh của hình vỏ hộp chữ nhật ta mang chu vi mặt đáy nhân với độ cao (cùng đơn vị đo).
(S_xq = (a + b) imes 2 imes h)
- mong tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.
(S_tp = S_xq + ,,S_day imes 2 = (a + b) imes 2 imes h + 2 imes a imes b)
Lưu ý:
- Chu vi dưới mặt đáy bằng tổng của chiều dài và chiều rộng lớn nhân với (2).
- Diện tích dưới đáy bằng tích của chiều dài với chiều rộng.
Ví dụ: Tính diện tích xung quanh và mặc tích toàn phần của hình vỏ hộp chữ nhật có chiều nhiều năm (8cm), chiều rộng (6cm) và chiều cao (4cm).
Giải:
Chu vi lòng của hình hộp chữ nhật là:
((8 + 6) imes 2 = 28;(cm))
Diện tích bao quanh của hình vỏ hộp chữ nhật đó là:
(28 imes 4 = 112;(cm^2))
Diện tích một đáy là:
(8 imes 6 = 48;(cm^2))
Diện tích toàn phần của hình hộp chữ nhật kia là:
(112 + 48 imes 2 = 208;(cm^2))
Đáp số: diện tích xung quanh: (112cm^2);
diện tích toàn phần: (208cm^2).
Chú ý: khi tìm diện tích s xung quanh ta hoàn toàn có thể làm gộp thành :((8 + 6) imes 2 imes 4 = 112cm^2) .
Xem thêm: Hướng Dẫn Cách Viết Địa Chỉ Bằng Tiếng Nhật Nhanh Nhất, Cách Viết Địa Chỉ Trong Tiếng Nhật


Chia sẻ
Bình chọn:
4.4 bên trên 691 phiếu
Luyện bài Tập Trắc nghiệm Toán lớp 5 - coi ngay
Báo lỗi - Góp ý
 |  |  |
TẢI app ĐỂ coi OFFLINE


Bài giải đang rất được quan tâm
× Báo lỗi góp ý
vấn đề em gặp phải là gì ?
Sai chính tả Giải khó hiểu Giải không nên Lỗi không giống Hãy viết cụ thể giúp Loigiaihay.com
gởi góp ý Hủy vứt
× Báo lỗi
Cảm ơn chúng ta đã sử dụng Loigiaihay.com. Đội ngũ gia sư cần cải thiện điều gì để bạn cho bài viết này 5* vậy?
Vui lòng nhằm lại thông tin để ad rất có thể liên hệ cùng với em nhé!
Họ cùng tên:
gởi Hủy quăng quật
Liên hệ cơ chế







Đăng ký kết để nhận lời giải hay và tài liệu miễn phí
Cho phép loigiaihay.com giữ hộ các thông tin đến chúng ta để nhận thấy các giải thuật hay cũng giống như tài liệu miễn phí.
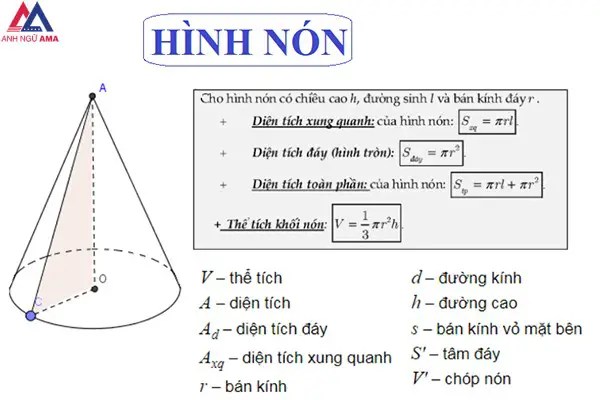
Trong hình học, diện tích xung xung quanh là trong số những khái niệm liên tục được sử dụng. Bài viết dưới đây của bọn chúng tôi hôm nay muốn giải đáp cho chúng ta cách tính diện tích xung quanh hình nón – một hình siêu hay chạm chán trong hình học không gian.
Hình nón là gì
Trước khi biết được công thức tính diện tích s xung quanh thì họ cần hiểu rõ hình nón là gì.
Trong hình học không gian, hình nón là 1 trong những hình có bề mặt phẳng và mặt phẳng cong phía lên phía trên. Đầu nhọn của hình nón được gọi là phần đỉnh, còn bề mặt phẳng được điện thoại tư vấn là phần đáy.
Trong đời sống hàng ngày, bạn cũng có thể dễ dàng phát hiện những đồ vật có ngoại hình nón như mẫu nón lá, cây kem ốc quế, nón sinh nhật,… Nó có 3 đặc điểm chính:
Có 1 đỉnh là hình tam giácCó 1 mặt tròn là phương diện đáy
Không có bất kỳ cạnh nào
Công thức tính diện tích xung xung quanh hình nón
Diện tích bao phủ của hình nón bao hàm diện tích phần phương diện xung quanh phủ bọc hình nón đó, không bao hàm phần diện tích đáy.
Diện tích bao quanh hình nón bằng tích của số Pi nhân với nửa đường kính đáy nhân với mặt đường sinh hình nón
Sxq = π.r.l
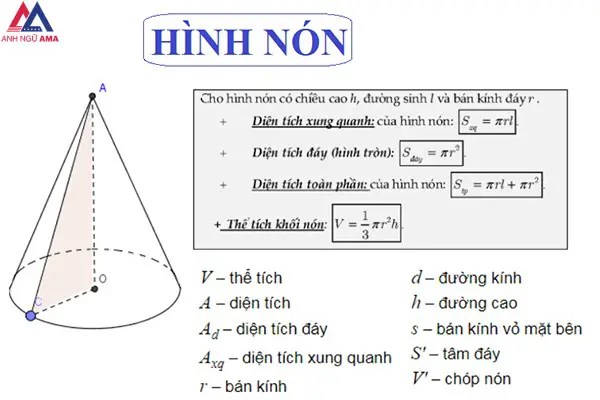
Trong đó:
– Sxq là diện tích xung quanh
– π là hằng số, bởi 3,14
– r là bán kính đáy
– l là độ dài con đường sinh
Hoặc hoàn toàn có thể áp dụng công thức sau: “Diện tích xung quanh hình nón bằng một nửa tích của chu vi mặt đường tròn lòng với độ dài con đường sinh.” bởi vì nửa chu vi mặt đường tròn chính là π.r.
Ví dụ: cho 1 hình nón gồm đáy là tâm O với đỉnh A. Độ dài nửa đường kính từ trọng tâm đáy hình nón tới một cạnh lòng là 7cm, chiều dài con đường sinh là 9cm. Hỏi diện tích s xung quanh mặt đường nón đó bằng bao nhiêu?
Đáp án: Sxq = π.r.l = 3,14.7.9= 197,82 (cm)²
Tham khảo thêm cỗ tài liệu Toán học tập của kynanggame.edu.vn
Các cách làm của hình nón
Công thức tính diện tích toàn phần của hình nón
Diện tích toàn phần của hình nón bao hàm toàn cỗ cả diện tích s xung quanh và mặc tích phần đáy tròn. Công thức:
Stp = Sxq + Sđáy = π.r.l + π.r^2
Công thức tính thể tích hình nón
Thể tích hình nón là toàn cục phần không gian mà nó chiếm, được xem bằng ⅓ tích của diện tích dưới đáy và chiều cao. Nuốm thể:
V hình nón = ⅓.π.r^2.h
Trong đó:
– V là thể tích
– π là hằng số, bởi 3,14
– r là nửa đường kính đáy
– h là mặt đường cao hạ từ bỏ đỉnh xuống đáy
Diện tích bao bọc hình nón cụt
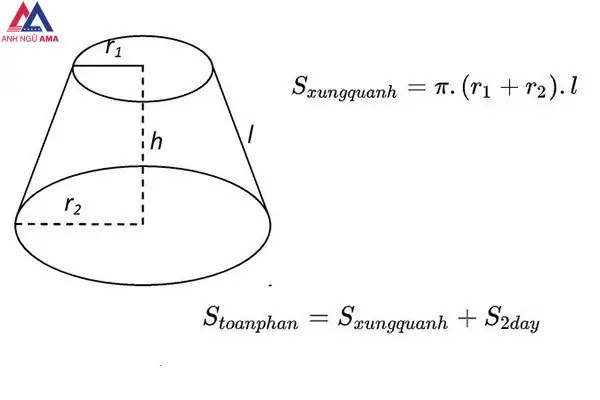
Hình nón cụt là một trong những hình bị giảm đi 1 phần của hình nón. Diện tích s xung xung quanh của hình nón cụt gồm phần diện tích mặt xung quanh, không bao hàm 2 diện tích s đáy.
Công thức tính diện tích s xung xung quanh của hình nón cụt
Sxq = π.(r1+r2).l

Trong đó:
– Sxq là diện tích xung quanh
– π là hằng số, bằng 3,14
– r1, r2 là nửa đường kính 2 đáy
– l là độ dài đường sinh
Diện tích toàn phần hình nón cụt
Stp = Sxq + S 2 đáy = π.(r1+r2).l + π.(r1)^2 + π.(r2)^2
Thể tích hình nón cụt
V = ⅓.π.h.((r1)^2 + (r2)^2 + r1.r2))
Cách tìm bán kính đáy, đường cao, con đường sinh của hình nón
Tìm mặt đường cao của hình nón
Đường cao là độ dài tính từ tâm dưới đáy đến đỉnh chóp của hình nón.
Công thức tính con đường cao của hình nón
h^2 = l^2 – r^2
Đường sinh của hình nón
Đường sinh bằng khoảng cách từ một điểm ngẫu nhiên trên mặt đường tròn đáy đến đỉnh của hình nón.
Độ dài mặt đường sinh của hình nón
l^2 = r^2 + h^2.
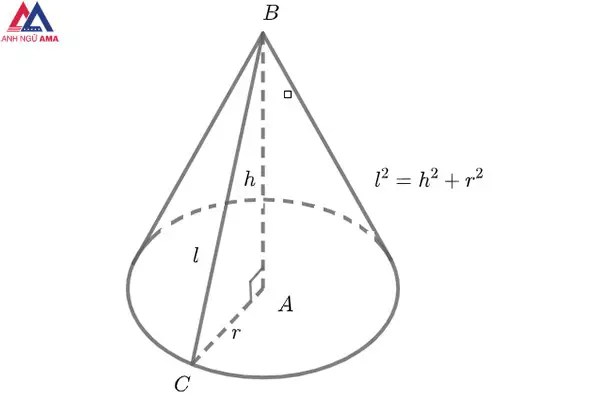
Bán kính đáy của hình nón
Chúng ta vẫn biết, hình nón được tạo nên thành khi ta cù tam giác vuông xung quanh trục một cạnh góc vuông của nó. Bởi vì vậy, nửa đường kính đáy và mặt đường cao có thể coi là 2 cạnh góc vuông của tam giác, và đường sinh vẫn là cạnh huyền. Cho nên vì vậy khi biết được 2 vào 3 dữ liệu này, ta có thể dễ dàng tính được số liệu còn lại. Vậy thể:
r^2 = l^2 – h^2
Bài tập tính diện tích s xung quanh của hình nón
Bài tập 1: Một hình nón có bán kính 4cm và chiều cao 7cm, tìm diện tích s xung quanh của hình nón.
Ở bài tập này, đầu tiên, ta phải tính được độ dài con đường sinh. Độ dài con đường sinh được tính theo công thức:
l^2 = r^2 + h^2
→ l = 8,06cm
Áp dụng công thức diện tích s xung xung quanh hình nón ta có:
Sxq = π.r.l
= π.4.8,06
= 101,23 cm2
Bài tập 2: cho thấy thêm diện tích toàn phần hình nón là 375 cm. Nếu đường sinh củai.nó gấp bốn lần chào bán kính, thì mặt đường kínhi.cơ sở của hình nón lài.bao nhiêu? áp dụng π = 3
Hướng dẫn giải như sau:
Theo đề bài: l = 4r và π = 3
Diện tích toàn phần hình nón là 375 cm2 buộc phải ta có: 3 × r × 4 r + 3 × r2 = 375
12r2 + 3r2 = 375
15r2 = 375
=> r = 5
Vậy bán kính dưới đáy hình nón là 5 => Đường kính khía cạnh nón là 5.2 = 10 cm.
Trên đấy là công thức tính diện tích bao phủ hình nón và một trong những công thức liên quan khác. Theo kinh nghiệm của kynanggame.edu.vn, uỳ trực thuộc vào đề bài cho những tài liệu nào mà bạn sẽ linh hoạt để tìm được đáp án chính xác.









